 Organic Priors in Non-Rigid Structure from Motion
Organic Priors in Non-Rigid Structure from Motion
Tel-Aviv, Israel.
Oral Presentation
(Top 2.7% of the papers)
 Organic Priors in Non-Rigid Structure from Motion
Organic Priors in Non-Rigid Structure from MotionThe problem of recovering the 3D shape of a non-rigidly deforming object from its image feature correspondences across multiple frames is widely known as Non-Rigid Structure from Motion (NRSfM). One of the popular ways to solve NRSfM is the matrix factorization approach. For this, a measurement matrix W is provided as input, which basically is a matrix of image feature correspondences augmented along the columns of W for each keypoint. Another way to think about it is that each column of W is a two-dimensional trajectory of a point across all the frames ---also referred to as trajectory space representation (see Figure b). The goal of NRSfM factorization approach under orthographic camera projection matrix assumption is to decompose the matrix W into product of two matrices R and S. Where, R, S must be a rotation matrix and shape matrix, respectively. Another general assumption is that the measurement matrix is already mean-centralized, so that the camera matrix reduces to pure rotation matrix. The problem is challenging due to the inherent unconstrained nature of the problem itself, as many 3D configurations can have similar image projections. To date, no algorithm can solve NRSfM for all kinds of conceivable motion. Consequently, additional constraints, priors, and assumptions are often employed to solve NRSfM using the matrix factorization approach.
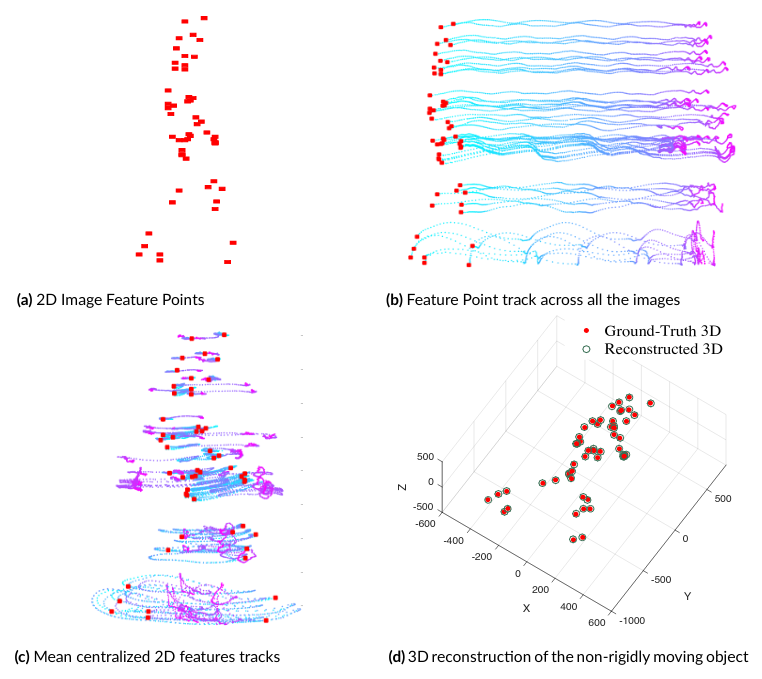
Figure. Classical NRSfM factorization setup.
In this paper, we coined the term "organic priors" for NRSfM. By organic priors, we mean the priors that reside in the factorized matrices, which are the results of natural mathematical steps in NRSfM matrix factorization. We show that such priors carry over within the intermediate factorized matrices, and its existence is independent of camera motion and shape deformation type. We used such a word to describe it because they come naturally by properly conceiving the algebraic and geometric construction of classical NRSfM factorization approach. Surprisingly, most existing methods, if not all, ignore them. Our work shows how to procure organic priors and utilize them effectively.
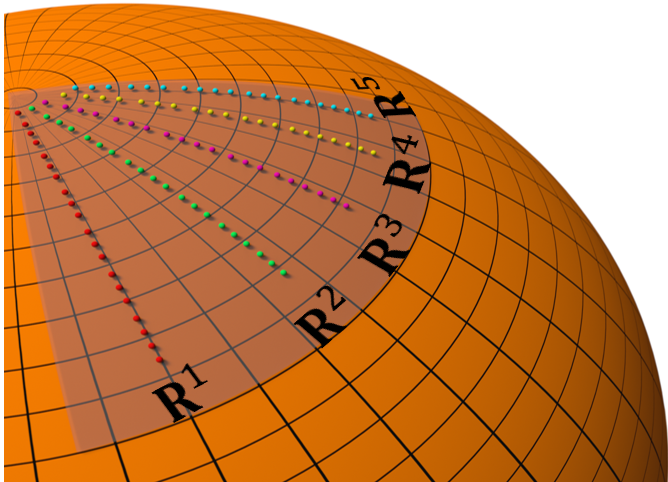
Figure. Organic Rotation Priors
@article{kumar2022organic,
title={Organic Priors in Non-Rigid Structure from Motion},
author={Kumar, Suryansh and Van Gool, Luc},
booktitle={European Conference on Computer Vision (ECCV)},
year={2022}
}


The authors thank Google for their generous gift ("ETH Zurich Foundation", 2020-HS-411).